공분산
위키백과 ― 우리 모두의 백과사전.
공분산(共分散, Covariance)은 확률론과 통계학분야에서 2개의 확률변수의 상관정도를 나타내는 값이다.(1개의 변수의 이산정도를 나타내는 분산과 는 별개임) 만약 2개의 변수중 하나의 값이 상승하는 경향을 보일 때, 다른 값도 상승하는 경향의 상관관계에 있다면, 공분산의 값은 양수가 될 것이다. 반대로 2개의 변수중 하나의 값이 상승하는 경향을 보일 때, 다른 값이 하강하는 경향을 보인다면 공분산의 값은 음수가 된다. 이렇게 공분산은 상관관계의 상승 혹은 하강하는 경향을 이해할 수 있으나 2개 변수의 측정 단위의 크기에 따라 값이 달라지므로 상관분석을 통해 정도를 파악하기에는 부적절하다. 상관분석에서는 상관관계의 정도를 나타내는 단위로 모상관계수 ρ를 사용한다.
목차[숨기기] |
공식 [편집]
실 수값을 지니는 2개의 확률변수 X와 Y에 대해서 공분산의 기대값E(X) = μ and E(Y) = ν은 아래와 같이 나타낼 수 있다.
기대값 연산자 E를 정리하면 아래와 같이 나타낼 수 있다.
만약 X와 Y가 통계적독립이라변 공분산은 0이 될것이고 이경우 아래와 같이 나타낼 수 있다.
2번째 식을 3번째식에 대입하면 아래과 같은 결과를 얻을 수 있다.
반대로 X와Y가 독립이 아니라면 위의 식은 성립하지 않는다.
Cov(X, Y)의 단위는 X와 Y의 곱이다. 상관관계는 공분산값을 필요로하며, 선형독립의 무원차수로 볼 수 있다.
공분산이 0인 확률변수를 비상관 확률변수라고 한다.
성질 [편집]
만약 X, Y가 실수값인 확률변수이고 a, b상수라면, 공분산에 대해서 아래와 같은 법칙이 성립한다.
확률변수인 X1, ..., Xn 과 Y1, ..., Ym에 대해서 아래와 같은 법칙이 성립한다.
확률변수인 X1, ..., Xn에 대해서 아래와 같은 법칙이 성립한다.
내적의 성질 [편집]
공분산의 많은 성질은 내적이 가지는 성질과 유사하다.:
- (1) 이중선형연산: 상수 a와 b 그리고 확률변수 X, Y, U, Cov(aX + bY, U) = a Cov(X, U) + bCov(Y, U)
- (2) 대칭성: Cov(X, Y) = Cov(Y, X)
- (3) 양수값: Var(X) = Cov(X, X) ≥ 0이고 Cov(X, X) = 0 이란 것은 X가 상수확률변수(K)라는 뜻이다.
공분산은 확률변수들의 벡터 공간 상에서의 내적을 의미한다. 벡터에서 적용되는 벡터합 X + Y 및 aX와 같은 스칼라곱의 성질도 지닌다.
공분산행렬 [편집]
열벡터값을 가지는 확률변수X 와 Y 가 각각 μ 와 ν라는 기대값을 가질 때 공분산벡터m×n 행렬은 아래와 같다.
벡터확률변수를 가지는 Cov(X, Y) 와 Cov(Y, X)는 각각의 전치행렬이다.
공분산은 때때로 2개의 확률변수간의 선형의존성을 나타내는 척도로도 사용된다. 이것은 선형대수에서 의미하는 선형의존성을 말하는 것은 아니다. 공분산을 정규화시키면 상관관계 행렬을 얻을 수 있다. 이로부터 Pearson Coefficient값을 얻을 수 있고 두개의 확률변수의 관계를 최적으로 설명가능한 선형함수를 표현가능하게 해준다. 이러한 점에서 공분산은 독립성이 선형척도로 볼 수 있다.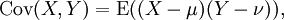










0 comments:
Post a Comment